Buckling and Design Optimisation of Vertical Tubes Subjected to External Concrete Pressures

Buckling and design optimisation of vertical tubes subjected to external concrete pressures

CONTENTS                                                                                                       .

1. ABSTRACT…………………………………………………………………………….1
2. INTRODUCTION
   1. Buckling……………………………………………………………………….1
   2. Euler………………………………………………………………………….2
   3. Plane Cylinder……………………………………………………………..3
3. LITERATURE REVIEW…………………………………………………………….4
4. METHODOLOGY……………………………………………………………………4
5. REFERENCES………………………………………………………………………….5

Abstract

Buckling is a phenomena that has been widely researched due to its nature and the devastating effects it can have. In civil engineering the main concerns are the safety of structures. There has been a lot of research carried out in the buckling of cylindrical shells that have been exposed to uniform external pressure. However the actual calculations that have been done are only specific to certain shell shapes, boundaries and loading conditions. This paper investigates a buckling analysis of a vertical tube subject to external pressures from concrete. In order to optimise the tube, the thickness can be increased and varied along the length of the tube. Additional methods of stiffening an existing tube will also be researched.

Introduction

Buckling

Buckling is defined as being a mathematical instability which leads to failure, it is a failure method that often ends up occurring quickly which makes it dangerous and can often be disastrous. Buckling is seen as being a bifurcation problem, this means that once a certain point has been reached after the load has been constantly increasing, any more load will result in more than one outcome. This can be either a compressed state of the member or a member that has buckled.

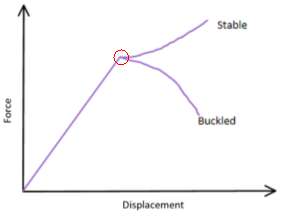
In the case of long and slender members, buckling is the main mode of failure. It occurs when the compressive loads on a member exceed a certain critical value. This results in a large sideways deflection being observed with a little increase in load above the critical load. The member is then said to have buckled.

Euler

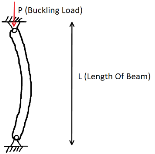The phenomena of buckling was first explained by Leonhard Euler and he determined the critical buckling load by considering simple beams with several different end support conditions. He devised an equation in order to calculate the critical buckling load:

${\mathrm{P}}_{\mathrm{cr}}=\frac{{\mathrm{\pi }}^2\mathrm{EI}}{{\mathrm{L}}^2}$

Where:

• P_cr is the critical buckling load (kN)
• E is the Young’s Modulus (GPa)
• I is the moment of inertia (mm⁴)
• L is the length of the member (m)

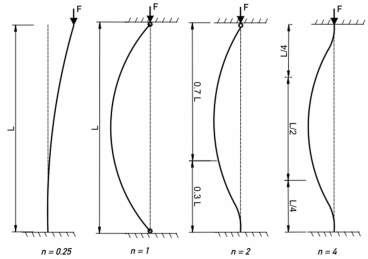
The above formula is used when the member is pinned at both ends. When there are differing end conditions for the member the equation becomes:

${\mathrm{P}}_{\mathrm{cr}}=\frac{{\mathrm{\pi }}^2\mathrm{EI}}{{(\mathrm{KL}}^2)}$

With k being the effective length factor which is calculated by using, $\mathrm{k}=\sqrt{\frac{1}{\mathrm{n}}}$

.  A value of less than 1 signifies that the structure is braced at one or more ends.

Plane Cylinder

When looking at the stability of a plane cylinder under external pressures there are four variables that come into play. The diameter of the cylinder, the larger the diameter the more stable the cylinder is. The length of cylinder, where a shorter length would provide more stability. The thickness of the cylinder is also considered with a thicker cylinder providing more stability. The material properties also play a part, with a higher modulus of elasticity giving more stability from elastic collapse.

When considering optimisations there are different methods that can be considered

When designing for an optimum shape, the easiest thing to do would be to increase the thickness of the shell in order for it to provide the required stability and an acceptable factor of safety.

Literature Review

There has been a lot of research done into buckling of cylindrical shells as it is a topic that proves to be an interest to a number of people. Due to the fact that the use of cylindrical shells is found in some way or another in a variety of industries. Numerous examples can be found online with each testing something different.

(R. Pinna, B. F. Ronalds, 2000) focused their studies on the buckling of shells that were subjected to hydrostatic loading.  They calculated the hydrostatic buckling load of a cylindrical shell with several boundary conditions. Comparisons were then made with existing results and also a number of finite element solutions.

(S. Kyriakides, T.A Netto, 1999) considered the buckling effects in long pipes that were exposed to a constant external pressure. They carried out their experiments in water or air to provide the constant pressure. They initiated the buckling at one end and observed the velocity. Analysing their results showed that a buckle travels faster in the air medium as opposed to water. This confirmed their theory that the fluid played a role.

(C.A Schenk, G.I. Schueller, 2002) studied the buckling of thin walled cylinders that had random geometric imperfections present. They made use of the Monte Carlo simulation alongside the finite element analysis

 Methodology

The first task required the conducting of research into buckling in order to further understand the problem at hand. In specific, focus was put on the buckling of plane cylinders subject to external pressures. Whilst

A finite element analysis software, LUSAS, was then used to map the problem…

Optimisations were carried out with the thickness being varied along the length…

References

• Forys, P. (2015). Optimization of cylindrical shells stiffened by rings under external pressure including their post-buckling behaviour. [online] Science Direct. Available at: https://0-www-sciencedirect-com.wam.city.ac.uk/science/article/pii/S0263823115300380 [Accessed 5 Jan. 2019].
• Kyriakides, S. (2000). On the dynamics of propagating buckles in pipelines. [online] Science Direct. Available at: https://0-www-sciencedirect-com.wam.city.ac.uk/science/article/pii/S0020768399003170  [Accessed 5 Jan. 2019].
• Lo Frano, R. (2012). Buckling of Thin Cylindrical Shell Subject to Uniform Exeternal Pressure. [online] Academia. Available at: www.academia.edu/27177507/Buckling_of_Thin_Cylindrical_Shell_Subject_to_Uniform_External_Pressure [Accessed 9 Jan. 2019].
• Matthew, P. (2016). Secant Formula. [online] Engineering Core Courses. Available at: http://www.engineeringcorecourses.com/solidmechanics2/C5-buckling/C5.2-secant-formula/theory/ [Accessed 7 Jan. 2019].
• Pinna, R. (2000). Hydrostatic buckling of shells with various boundary conditions. [online] Science Direct. Available at: https://0-www-sciencedirect-com.wam.city.ac.uk/science/article/pii/S0143974X99001042 [Accessed 5 Jan. 2019].
• Sönnerlind, H. (2014). Buckling, When Structures Suddenly Collapse. [online] COMSOL. Available at: https://www.comsol.com/blogs/buckling-structures-suddenly-collapse/  [Accessed 9 Jan. 2019].
• Steel-insdag.org. (2019). [online] Available at: http://steel-insdag.org/TeachingMaterial/Chapter6.pdf  [Accessed 04 Jan. 2019].