Introduction
1.1 Reviewing of General Relativity
1.1.1 Metric Tensor
The equation which describes the relationship between two given points is called metric and is given by


Where  interval of space-time between two neighboring points,
interval of space-time between two neighboring points,  connects these two points and are the components of contra variant vector. Through the function
connects these two points and are the components of contra variant vector. Through the function , any displacement between two points is dependent on the position of them in coordinate system.
, any displacement between two points is dependent on the position of them in coordinate system.
The displacement between two points in rectangular coordinates system is independent of their components due to homogeneity, so metric is given by

Where 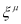 are the space-time coordinates,
are the space-time coordinates,  is speed of light and
is speed of light and  is metric for this case and is given by
is metric for this case and is given by

Through the coordinates transformation from rectangular coordinates, , to curved coordinates system the components of
, to curved coordinates system the components of in a curved coordinates system can be found . For constructing rectangular coordinates system in a curved coordinates if space-time is locally flat then it is possible to that locally. From rectangular coordinates system
in a curved coordinates system can be found . For constructing rectangular coordinates system in a curved coordinates if space-time is locally flat then it is possible to that locally. From rectangular coordinates system defined locally in a point of a curved space-time to a curved coordinates system
defined locally in a point of a curved space-time to a curved coordinates system  can be written as
can be written as

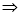

So in this way we can find local values of metric tensor
Three important properties of metric tensor are:
 is symmetric
is symmetric so we have
so we have

- metric tensors are used to lowering or raising indices
1.1.2 Riemann Tensor, Ricci Tensor, Ricci Scalar
The tool which plays an important role in identifying the geometric properties of spacetime is Riemann (Curvature) tensor. In terms of Christoffel symbols it is defined as:

Where  .If the Riemann Tensor vanishes everywhere then the spacetime is considered to be flat. In term of spacetime metric Riemann Tensor can also be written as:
.If the Riemann Tensor vanishes everywhere then the spacetime is considered to be flat. In term of spacetime metric Riemann Tensor can also be written as:
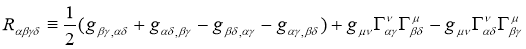
thus useful symmetries of the Riemann Tenser are:


so due to above symmetries, the Riemann tensor in four dimensional spacetime has only 20 independent components. Now simply contracting the Riemann Tensor over two of the indices we get Ricci Tensor as:

above equation is symmetric so it has at most 10 independent components. Now contracting over remaining two indices we get scalar known as Ricci Scalar.

Another important symmetry of Riemann Tensor is Bianchi identities
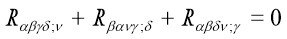
This after contracting leads to
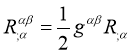
1.1.3 Einstein Equation
The Einstein equation is the equation of motion for the metric in general theory of relativity is given by:

Where  is stress energy momentum tensor and
is stress energy momentum tensor and 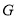 is Newton’s constant of Gravitation. Thus the left hand side of this equation measures the curvature of spacetime while the right hand side measures the energy and momentum contained in it.Taking trace of both sides of above equation we obtain
is Newton’s constant of Gravitation. Thus the left hand side of this equation measures the curvature of spacetime while the right hand side measures the energy and momentum contained in it.Taking trace of both sides of above equation we obtain
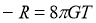
using this equation in eq. ( ), we get


In vacuum  so for this case Einstein equation is
so for this case Einstein equation is
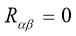
We define the Einstein tensor by

Taking divergence of above eq. we get

1.1.4 Conservation Equations for Energy momentum Tensor
In general relativity two types of momentum-energy tensor,are commonly used: dust and perfect fluid.
1.4.1 Dust: It is simplest possible energy-momentum tensor and is given by
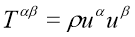
The 4-velocity vector for commoving observer is given by
 , so energy momentum tensor is given by
, so energy momentum tensor is given by

It is an approximation,of the universe at later times when radiation is negligible
1.4.2 Perfect fluid: If there is no heat conduction and viscosity then such type of fluid is perfect fluid and parameterized by its mass density and pressure and is given by

It is an approximation of the universe at earlier times when radiation dominates so conservation equations for energy momentum tensor are given by

In Minkowski metric it becomes

1.1.5 Evolution of Energy-Momentum Tensor with Time
We can use eq. () to determine how components pf energy-momentum tensor evolved with time. The mixed energy-momentum tensor is given by:

and its conservation is given by

Consider  component:
component:

Now all non-diagonal terms of  vanish because of isotropy so
vanish because of isotropy so  in the first term and
in the first term and  in the second term so
in the second term so

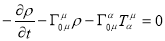
For a flat, homogeneous and isotropic spacetime which is expanding in its spatial coordinate’s by a scale factor , the metric tensor is obtained from Minkowski metric is given by:
, the metric tensor is obtained from Minkowski metric is given by:

The Christoffel symbol by definition
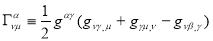

 Because
Because 
 Because
Because  the only non-zero
the only non-zero  is
is  so from eq. () conservation law in expanding universe becomes
so from eq. () conservation law in expanding universe becomes

 after solving above equations we get
after solving above equations we get

above equation is used to find out for both matter and radiation scale with expansion. In case of dust approximation we have  so
so

So energy-density of matter scale varies as  .Now the total amount of matter is conserved but volume of the universe goes as
.Now the total amount of matter is conserved but volume of the universe goes as  so
so 
In case of radiation so from eq.() we obtain
so from eq.() we obtain
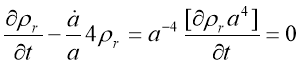
Which implies that , science energy density is directly proportional to the energy per particle and inversely proportional to the volume, that is,
, science energy density is directly proportional to the energy per particle and inversely proportional to the volume, that is,  because
because  so the energy per particle decreases as the universe expands.
so the energy per particle decreases as the universe expands.
1.2 Cosmology
In physical cosmology, the cosmological rule is a suspicion, or living up to expectations theory, about the expansive scale structure of the universe. Throughout the time of Copernicus, much data were not accessible for the universe with the exception of Earth, few stars and planets so he expected that the universe might be same from all different planets likewise as it looked from the Earth. It suggests isotropy of the universe at all focuses. Once more, a space which is isotropic at all focuses, is likewise homogeneous. Copernicus rule and this result about homogeneity makes the Cosmological rule (CP) which states that, at a one-time, universe is homogeneous and isotropic. General covariance ensures validity of Cosmological Principle at other times also.
1.2.1 Cosmological metric:
Think about a 3D circle inserted in a 4d “hyperspace”:

where  is the radius of the 3D sphere. The distance between two points in 4D space is given by
is the radius of the 3D sphere. The distance between two points in 4D space is given by

solving we get

now becomes

In spherical coordinates


Finally we obtain

We could also have a saddle with or a flat space. In literature shorthanded notation is adapted:



To isolate time-dependent term, make the following situation:

Then

where

If we introduce conformal time (arc parameter measure of time) as


then we can express the 4D line element in term of FRW metric:

1.2.2 Friedmann Equation:
We can now figure out Einstein field mathematical statement for perfect fluid. All the calculations are carried out in comoving frame where


and energy-momentum tensor is given by
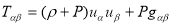
Raising the index of the Einstein tensor equation

we get


After contracting over indices  and
and  we get
we get


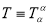
so Einstein’s Equation can be written as

It is easily found for perfect fluid


finally we obtain the components of Ricci tenser



The  components are
components are


and  components are
components are

To get a closed system of equations, we need a relationship of equation states which relates
which relates and
and  so solving
so solving



At this point when we joined together with equation 62 comparisons in the connection of energy-momentum tensor and the equation of states, we get a closed frame work of Friedmann equations:





1.2.3 Solutions of Friedmann Equations:
We are going to comprehend Friedmann equation for the matter dominated and radiation dominated universe and get the manifestation of scale factor. From the definition of Hubble’s law





Matter Dominated Universe: : It is showed by dust approximation 

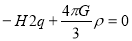





As both  and
and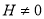 , for flat universe (
, for flat universe ( ),
),  (
(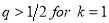 an
an ) for
) for  . When combined with equation, this yields critical density
. When combined with equation, this yields critical density
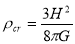
Currently it value is  (we used
(we used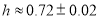 ).The quantity
).The quantity  provide relationship between the density of the universe
provide relationship between the density of the universe  and the critical density so it is given by
and the critical density so it is given by 
Now the second Friedmann equation for matter dominated Universe becomes
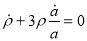




so lastly

Radiation-dominated Universe: It is showed by perfect fluid approximation with 
The second Friedmann Equation becomes


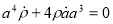


Flat Universe 
Matter Dominated Universe (dust approximation) 
The first Friedmann equation becomes



At the Big bang  Using convention
Using convention  and universe flat condition
and universe flat condition  we finally get
we finally get


Now we can calculate the age of universe , which corresponds to the Hubble rate
, which corresponds to the Hubble rate  and scale factor
and scale factor 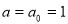 to be:
to be:
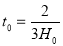
Taking  and
and  we get
we get
 Years
Years
Radiation-dominated:
The First Friedmann equation becomes



 At the big bang
At the big bang  and
and  .Also we have
.Also we have 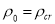

Closed Universe 
Matter-dominated
The first Equation becomes




In term of conformal time we can rewrite the above integral as

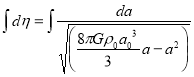
After substituting  and using equation
and using equation

Then 
but we have 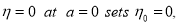 so we get
so we get

 .
.
Now

but we have  at
at  sets
sets . So we have now the dependence of scale factor
. So we have now the dependence of scale factor  in term of the time
in term of the time 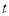 parameterized by the conformal time
parameterized by the conformal time  as
as


Radiation-dominated Universe:
The first Friedmann equation becomes
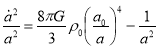


In term of conformal time we can re write the integral as 

but we have conditions 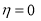 at
at 
 sets
sets  so we get
so we get


and the requirement 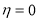 at
at  sets
sets  , finally we have
, finally we have


Open Universe 
Matter-dominated (dust approximation):
The first Friedmann equation 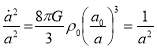


In term of conformal time we can rewrite the integral as

Take
Cite This Work
To export a reference to this article please select a referencing style below:


