Factors Affecting The Weight a Column Can Withstand

Matthew Keeley 

Physics EEI

This extended experimental investigation explores the weight a paper column can withstand before it buckles and how changing the diameter, length and thickness of a column affects its critical load. Multiple columns with varying diameters, lengths and thicknesses were constructed and each one had masses added to it until it buckled. The hypotheses “If the diameter of a paper column is increased, then the weight the paper column can withstand before buckling will also increase exponentially” and “If the length of a paper column is decreased, then the weight the paper column can withstand before buckling will increase exponentially” were not supported while the hypothesis “If the thickness of a paper column is increased, then the weight the paper column can withstand will also increase proportionally” was supported.

Get Help With Your Essay

If you need assistance with writing your essay, our professional essay writing service is here to help!

Essay Writing Service

Columns are used in architecture and structural engineering, in the walls of houses and buildings, to transmit weight through compression from the structure above the column to the structural elements beneath (Merriam-webster.com, 2017). Objects are only referred to as columns when the force is applied axially; they are referred to as beams otherwise (Waddell, 1925). Column buckling is likely the only area of structural mechanics where failure is not due to the strength of the material, but the stiffness of the material and the shape of the column instead (McGinty, 2017). Buckling occurs in a column when its critical load is reached and this value can be determined by the Euler column formula, which is as follows:

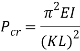
Where 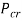is the critical load (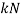), 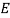is the modulus of elasticity (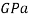), 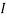is the area moment of inertia (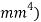, 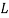is the length of the column (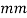) and 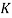is the column effective length factor (Engineeringtoolbox.com, 2017). Engineers commonly use mm instead of regular SI unit, examples of the formula being used use mm (Critical Buckling Load (Example 1) – Mechanics of Materials, 2013).

This formula is used mainly to calculate the buckling load of steel and wooden columns so its application in the buckling of paper columns is questionable although it is the only method available.

There are some unknown values in the equation without researching them using other sources, the 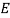value, the 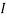value and the 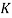value.

The 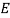value, the modulus of elasticity (also known as young’s modulus, the elastic modulus or the tensile modulus) is a constant that is a measure of the stiffness of a material (Askeland et al., 1996). It is the slope of the stress-strain curve in the elastic region given by:

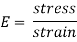
A relationship known as Hooke’s Law, Hooke’s law states that the strain in a solid is proportional to the applied stress within the elastic limit of that solid (Encyclopedia Britannica, 2017). For example, if an object with a high modulus of elasticity had the same force applied to it as an object with a low modulus of elasticity there would be a greater change in dimension in the object with the smaller modulus of elasticity.

The modulus of elasticity is represented in pascals (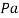) but the value is usually very large so it is found in gigapascals instead (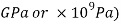. When calculating theoretical data to keep the units the same the modulus of elasticity was represented in 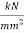as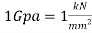. The modulus of elasticity for paper is 2 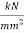(www-materials.eng.cam.ac.uk, 2017).

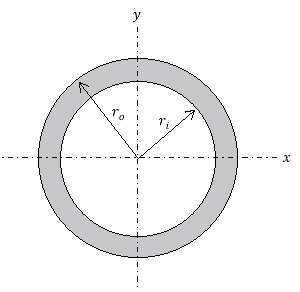
The 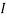value represents area moment of inertia (also known as second moment of area). It is a geometrical property of an area representing how its points are distributed regarding an axis within the object (Beer and Johnston, 1990). It is calculated using multiple integral over the columns cross-section, but it’s easier to utilise an already existing formula for the second moment of area of the column in question. Since the column that will be used in the experiment is rolled up paper it will have a hollow cylindrical cross-section which will appear as:

The formula for second moment of area for a hollow cylindrical cross-section is as follows:

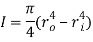
Where 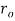is the radius of the outside circle and 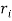is the radius of the inside circle (Efunda.com, 2017).

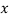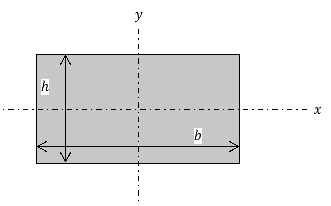
The second moment of area also determines the way a column is most likely to buckle (towards the plane or the plane). Usually there would be multiple formulae for the second moment of area, one for buckling towards the plane and one for buckling toward the 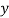plane, but since the cross section in question is hollow cylindrical and the axis (where the weight will be applied) is in the centre of the cross-section the formulae are identical. If the cross section was a filled rectangular area, for instance, and appeared as:

Then the formulae for second moment of area are as follows:

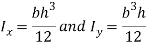
One would have to solve for both 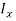and 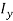and find out on which plane the column is most likely to buckle along and use that value as the second moment of area in the Euler column formula (What is second moment of area?, 2015). The units for second moment of area are metres to the fourth power (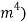, but since the units need to be kept the same and the radius will be represented in millimetres when doing theoretical data, it will be in millimetres to the fourth power (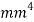) instead.

The last unknown value is 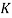which is the column effective length factor (Wai-Fah and Duan, 1999). It is determined by the boundary conditions. The value changes depending on if the column is fixed on both ends, hinged on both ends, fixed on one end free on another, etc. The columns used in the experiment are free on both ends so the theoretical 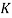value is 1, but the actual 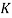value derived from various other experiments is 1.2, so that value will be used in theoretical data (Efunda.com, 2017).

For this experiment to be a success many variables must be remain the same that were quite difficult to control. To attempt to control these variables some precautions were taken. For example, to keep the distribution of weight the same a transparent board was used so the weight could be placed in the centre of the column and distributed evenly. Also, the paper columns need to be made carefully so that there are no weaknesses in the column because weaknesses in the column aren’t factored into Euler’s column formula. The dimensions for paper are 29.7mm x 21mm x 0.1mm (for 80gsm A4 paper).

Theoretical Data

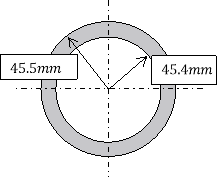
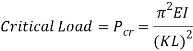
Calculating second moment of area ().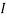

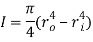
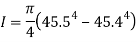
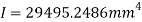
Substituting into Euler’s column formula and solving to find critical load.

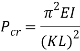
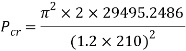
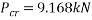
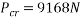
Calculating the mass the column could withstand using .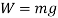

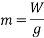
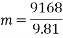
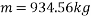
This value is very large and a paper column of the dimension used in the calculations would certainly crumble under this amount of force in real life applications, but this may be due to all the other variables that are difficult to control at play, such as weaknesses in the column geometrically and weight distribution rather than the formula being incorrect.

Theoretical data results tables and graphs

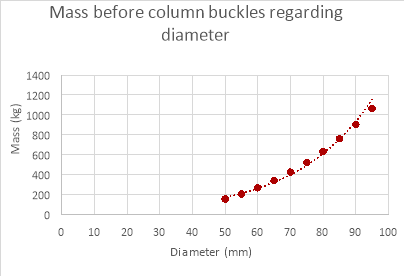Changing Column’s diameter

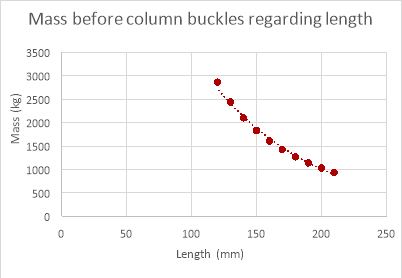
Changing Column Length

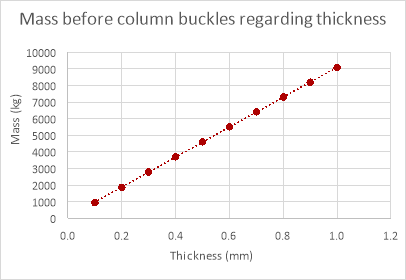Changing Column’s Thickness

The following hypotheses that were prompted due to the background research are as follows:

Changing Column’s Diameter

If the diameter of a paper column is increased, then the weight the paper column can withstand before buckling will also increase exponentially.

Changing Column’s Length

If the length of a paper column is decreased, then the weight the paper column can withstand before buckling will increase exponentially.

Changing Column’s Thickness

If the thickness of a paper column is increased, then the weight the paper column can withstand will also increase proportionally.

Changing Column’s Diameter

Various paper columns were constructed carefully (as to reduce weak points in the column) with different diameters, starting at 9.5cm diameters reducing the diameter by 0.5cm for every column until 10 columns had been made, so that there was enough variation in the data to develop more accurate results. The column with the smallest diameter had a diameter of 5cm. The experiment was then set up like the diagram on the previous (without the weights). The board on the bottom of the column was set up to protect the bench from damage from the falling weights and a small transparent board was placed on top of the column so that the weights could be accurately placed in the centre of the column to keep the distribution of weight even.  50g masses were then added to the column until it buckled and the mass that is buckled at was graphed for later analysis. This process was completed for all the columns made beforehand and the experiment was repeated until 3 trials had been completed so the data discovered was more accurate.

Changing Column’s Length

Paper columns with various lengths were constructed carefully, starting at a length of 21cm and reducing by 1cm until 10 columns had been made, so there was enough variation in the data to provide more accurate results. The column with the smallest length had a length of 12cm. The experiment was then set up like the diagram (without the weights). The board on the bottom of the column was set up to protect the bench from damage from the falling weights and a small transparent board was placed on top of the column so that the weights could be accurately placed in the centre of the column to keep the distribution of weight even.  50g masses were then added to the column until it buckled and the mass that is buckled at was graphed for later analysis. This process was completed for all the columns made beforehand and the experiment was repeated until 3 trials had been completed so the data discovered was more accurate.

Changing Column’s Thickness

Paper columns with varying thicknesses were constructed by taping pieces of paper together (1 piece of paper has a thickness of 0.1mm, 2 taped together 0.2mm, etc.) until 10 columns had been made, so there was enough variation in the data to provide more accurate results. The experiment was then set up like the diagram (without the weights). The board on the bottom of the column was set up to protect the bench from damage from the falling weights and a small transparent board was placed on top of the column so that the weights could be accurately placed in the centre of the column to keep the distribution of weight even.  50g masses were then added to the column until it buckled and the mass that is buckled at was graphed for later analysis. This process was completed for all the columns made beforehand and the experiment was repeated until 3 trials had been completed so the data was more accurate.

Variables

Dependent Variable

The independent variable is the mass the column can withstand before it buckles, as this is what the experiment is testing and what changes when the independent variables are manipulated.

Independent Variables

The independent variables in this experiment are the ones that get changed, the diameter, the length and the thickness. Changing these will affect the dependent variable.

Controlled Variables

The controlled variables are everything that was kept the same during the experiment, although these may have changed regardless of efforts to keep them the same during the experiment. They include: the temperature and pressure, brand of paper, consistency of columns, distribution of weight, wind conditions, material of column, weights that were used, elevation and the material experiment was performed on.

Safety

When the column buckles, the weights will fall off the column and potentially an injury could occur. To deal with this the falling weights must be avoided and people entering the area of the experiment should be careful walking through. A mechanism to catch the board so the weights don’t fall could also be constructed.

Scissors could potentially be used to cut someone. To deal with this the scissors were treated with caution and used appropriately. Wearing goggles will also protect the eyes.

Changing Column’s Diameter

Changing Column’s Length

Changing Column’s Thickness

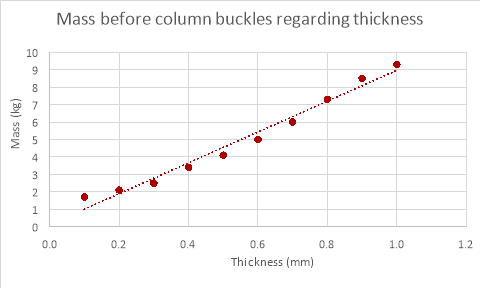
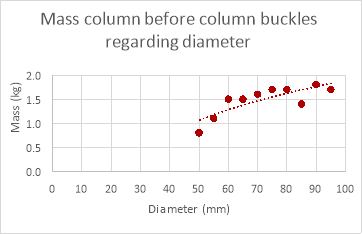
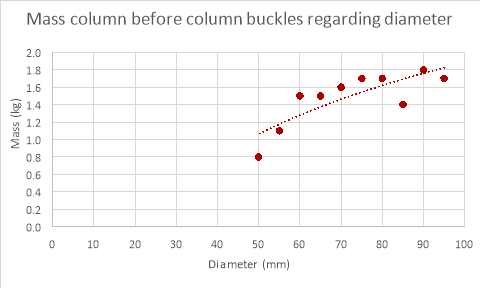
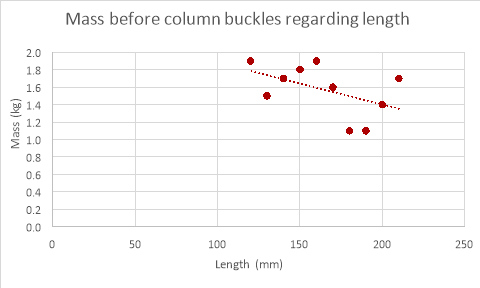
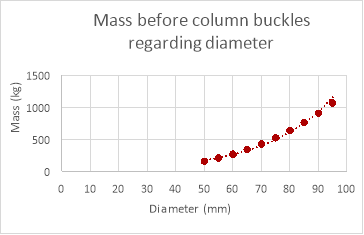The results for changing column diameter seem to have a pattern to them, the weight that the column can support increases with diameter, but while the mass the column could withstand changed with diameter the increments in which the value changed reduced every time the diameter increased (logarithmic relationship). The results for changing the length of the column provided results that were expected, the weight the column could withstand decreased as the length of the column was decreased though a proper relationship between the points was underivable. The results for the thickness of the column were as expected, the mass the column could withstand increased proportionally with the thickness of column.

As evident by the graphs above the theoretical data differs greatly to the empirical data. The theoretical data shows an exponential relationship between the mass withstood and the diameter of the paper column while the empirical data shows a more logarithmic relationship (if the experiment was continued further the mass withstood would have continued to increase with diameter). The mass the column can withstand is also much larger in the theoretical data than the empirical data. This is because the theoretical calculations don’t factor in the weaknesses in the column geometrically and its extremely unlikely that the distribution of mass was perfect, even if the mass was placed a millimetre off the axis the mass the column could withstand would decrease drastically. Therefore, it would be difficult to get empirical results the same as the theoretical data due to many variables that are nearly impossible to control when dealing with paper columns.

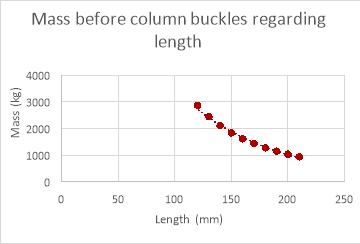
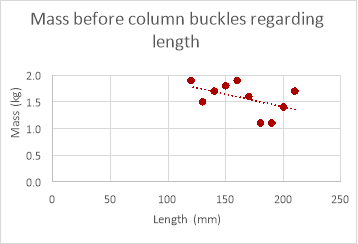
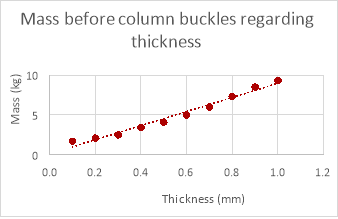
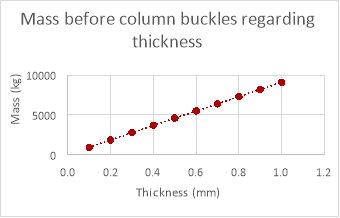As shown in the graphs above the mass the column can withstand does decrease as length increases in the empirical data but is hard to decipher a relationship when looking at the empirical data due to anomalies. These anomalies would yet again be caused by variables that are too difficult to control within the experiment and for the same reasons the mass the column can withstand in the theoretical data is much greater than the mass the column could withstand in reality.

The relationship between these two sets of data is identical (both increasing proportionally) although the mass the column could withstand theoretically is much greater than the mass it could withstand empirically. A possible reason that the relationship was evident in the empirical data for changing the thickness of the column and not for changing the diameter and length could be that changing the thickness affects the mass the column can withstand much more than changing either the length of the column or its diameter (reducing anomalies), this is evident when comparing the theoretical data for the three variables.

Due to the varying relationships found in the empirical data and the complexity of the formula used it is difficult to relate Euler’s column formula to existing mathematical models when looking at changing the column’s diameter or length because the relationship is either exponential (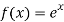) or logarithmic (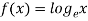). Euler’s column formula can be related to the linear function that is found when changing the column’s thickness though.

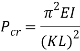
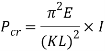
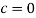because a column with 0 length, diameter or thickness