A discussion and comparison of the radial velocity method and the transit photometry method of detecting exoplanets.
An exoplanet is a planet that is outside of our solar system orbiting another star, and so far (at 15/01/2017) 3560 exoplanets have been detected [1]. Currently, with modern technology, the two main ways of detecting an exoplanet is using either the radial velocity method or the transit photometry method, both of which having their advantages and disadvantages. Radial velocity works by the exoplanet having a gravitational effect on the star it is orbiting causing the star to move slightly, leading to its detected light spectra being periodically shifted between red-shift and blue-shift as the planet orbits it. The minimum mass can then be calculated from the star's light spectra. Transit photometry can be used to detect exoplanets by observing a periodic reduction in the intensity of light detected from a star caused by the planet going directly in front of it between the star and the earth. The size of the planet can be worked out by measuring the decrease in light and sometimes the composition of the planet can be deduced
Get Help With Your Essay
If you need assistance with writing your essay, our professional essay writing service is here to help!
The radial velocity method, also known as the Doppler spectroscopy method, to detect exoplanets was the first proper method that worked effectively. Orbiting planets cause a star to move slightly due to their gravitational pull, since the planet has mass. This slight movement of the star being orbited affects the light spectrum from that star which is received by observers on Earth. Regular periodic shifts in the star's expected spectrum, which would appear as a "wobble", indicates the presence of an orbiting planet [2]. If the exoplanet caused the star to move towards Earth then its light spectrum would be blue shifted, if the star moved away from Earth the spectrum would be red shifted.
The mass of the orbiting planet can then be determined, as Kelper's third law of planetary motion can be used to determine the orbital radius of the planet from the mass of the star, calculated using a Hertzsprung-Russell diagram, and the orbital period of the planet determined from the star's light spectrum. Then Newton's law of gravitation and the orbital law can be used to derive the equation
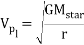
to calculate the velocity of the orbiting planet. With the velocity of the planet, the equation
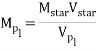
can be used to work out the mass of the detected planet [3].
Using radial velocity is the most common method used to date to detect exoplanets, it has the advantage of not necessarily a very long time comparative to the other methods and is thus useful in large scale surveys to find multiple exoplanets. Unfortunately, it does not give much specific information about the planet itself and hence must be combined with other techniques to obtain information like the planet's chemical composition, density, and volume. Other methods could thus have more potential for the future for more in depth analysis of the detected planet [4].
One major complication with radial velocity is that it is difficult tell mass of a detected planet easily, only the minimum mass based on how much star appears to move can be calculated, as it depends on the angle of the orbital plane of the planet. If the angle, θ, is the angle made by the plane perpendicular to the orbit of the planet from the plane of the sight from Earth, then the component in line with Earth is sin(θ). The detected mass, M, is thus the product of the actual mass of the planet and sin(θ). The larger θ, where 0 < θ < π/2, the more accurate the calculated mass is and so would be very close to the actual mas of the planet. As θ approaches 0, the calculated value of M becomes less accurate and closer to zero itself, hence only the minimum for M is known, the actual value could be much larger. Regrettably for astronomers, it is very rare to know the true value of θ since it cannot always be seen or calculated from the star's light spectrum [5]. This gives arise to the problem that on a rare occasion a low mass star can be detected in a binary star system and mistaken for a planet due to a mass being calculated much smaller than its actual mass and thus appears more similar to that of a planet because of the plane of its orbit with respect to earth.
This method mainly detects planets that are very close to the star, massive, and have very short orbital periods so cause the largest wobbles that don't take very long to detect. Planets like this are often referred to as "hot Jupiters", due to them being of similar size, mass, and composition to that of the planet Jupiter in our solar system but they are much closer to the star they are orbiting, hence being hotter [6]. A downside of this is that one of the main purposes of detecting exoplanets is to find planets capable of supporting life, and hot Jupiters are very unlikely to do this.
Another main method of detecting exoplanets is called transit photometry. A planet may be detected by taking measurements of the dimming of light emitted by the star it orbits. When the planet passes directly in front of the star, as seen from Earth, it blocks out a fraction of the light that we receive. If this dimming occurs at regular intervals, then it may be deduced that this planet is in orbit and passing in front of the star once every orbital period [7].
The amount of dimming that occurs reflects the ratio of size between the star and planet; since the size of such a star may be determined from its spectrum we may then estimate the planet's size. For planets orbiting the same sized star with the same luminosity and same light emission spectra, planets orbiting it will decrease the amount of light received on earth by different amounts depending on the size of the planets [8]. A planet with a radius three times larger than another orbiting planet will lead to a drop in the amount of light received nine times that of the other planet. Hence, the decrease in light received from the star due to a planet's transit is proportional to the square of the planet's radius and so proportional to the planet's cross-sectional area.
When this method is combined with radial velocity analysis which gives an estimated mass, the density may be calculated, giving a much clearer picture of the composition of the planet. The planet's atmospheric conditions may also be uncovered by analysing the depth of the transit at different wavelengths of light. Light emitted by the star will be absorbed by gases in the planet's atmosphere to different degrees at different wavelengths [9]. Therefore, by studying its spectra elements in the atmosphere may be determined. For such analysis to be carried out, searches must continuously cover large portions of the sky and its cluttered light sources over long periods of time.
Transit photometry only works, however, when a planet passes directly between its star and the Earth, which is uncommon. For a star one astronomical unit (approximately about 150 million kilometres) away from its star, and the star being the same as the sun earth orbits, the probability of an orbiting planet producing a detectible transit is 0.47%, given that the planet has a random orbital alignment [10]. A planet's orbital period could be a very long time, months, or years, but its transit directly in front of the star between it and earth could only be a couple of hours. Despite this, in very large scale exoplanet finding surveys spanning over extended periods of time and covering potentially thousands of stars, the transit photometry method has been found to be more effective than the radial velocity method at finding a larger number of exoplanets [11]. However, transit photometry has a much larger detection rate of "false positives", meaning an exoplanet was thought to be detected using this method but after further investigation was found to be a false detection. A 2012 study found that in single planetary systems, the number of false detections was up to 40%, based on the observations from the Kepler mission [12]. This means that, in the case of single planetary systems, a planetary detection using transit photometry must be verified using another method, which is often radial velocity and sometimes the less common method of orbital brightness modulation.
References
[1] Schneider, J. 2017. Interactive Extra-Solar Planets Catalogue. The Extrasolar Planets Encyclopedia. [Online]. [Accessed 15/01/2017]. Available from: http://exoplanet.eu/catalog/
[2] Astronomy Notes. 2007. The Velocities of Stars. [Online]. [Accessed 15/01/2017]. Available from: http://www.astronomynotes.com/starprop/s8.htm
[3] Fischer, D. 2010. Radial Velocity. Yale University. [Online]. [Accessed 15/01/2017]. Available from: http://exoplanets.astro.yale.edu/workshop/EPRV/Bibliography_files/Radial_Velocity.pdf
[4] Zechmeister, M. 2011. Precision radial velocity surveys for exoplanets. 1st ed. [S.l.: s.n.].
[5] The Planetary Society. 2016. Radial Velocity. [Online]. [Accessed 15/01/2017]. Available from: http://www.planetary.org/explore/space-topics/exoplanets/radial-velocity.html
[6] Sasselov, D. 2008. Astronomy: Extrasolar planets. Nature. 451(7174). pp.29-31.
[7] Shannon, L. and Russell, D. 2012. Exoplanet Transits: Light Curve Photometry. Bangor University. [Online]. [Accessed 15/01/2017]. Available from: http://www.baylor.edu/content/services/document.php/181811.pdf
[8] The Planetary Society. 2016. Transit Photometry. [Online]. [Accessed 15/01/2017]. Available from: http://www.planetary.org/explore/space-topics/exoplanets/transit-photometry.html
[9] Shore, L. 2014. Searching for Exoplanets. Exploratorium Teacher Institute. [Online]. [Accessed 15/01/2017]. Available from: http://www.exo.net/~pauld/Venus/ExoPlanets%20and%20Transits.pdf
[10] Carroll, M. 2017. Earths of Distant Suns. 1st ed. Cham: Springer International Publishing. p.50.
[11] Hidas, M. et al. 2005. The University of New South Wales Extrasolar Planet Search: methods and first results from a field centred on NGC 6633. Monthly Notices of the Royal Astronomical Society. 360(2). pp.703-717.
[12] Santerne, A., Díaz, F., Moutou, C., Bouchy, F., Hébrard, G., Almenara, M., Bonomo, S., Deleuil, M., Santos, C. 2012. SOPHIE velocimetry of Kepler transit candidates. Astronomy & Astrophysics. 545. p.A76.
Cite This Work
To export a reference to this article please select a referencing style below:


